Aufgaben II
Beispiel
Das Integral 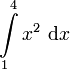 berechnet sich mit Hilfe des Hauptsatzes der Differential- und Integralrechnung wie folgt:
berechnet sich mit Hilfe des Hauptsatzes der Differential- und Integralrechnung wie folgt:
![\int\limits_1^4 x^2 \ \mathrm{d}x = \left[ \frac{1}{3} x^3 \right]_1^4 = \frac{1}{3} \cdot 4^3 - \frac{1}{3} \cdot 1^3 = \frac{64}{3} - \frac{1}{3} = 21](Integral11-Dateien/fbac4725281d4dbba482e70719992c05.png) .
.
|
Berechne das bestimmte Integral! |
|
Berechne das Integral. |
|
Berechne die Fläche zwischen dem Graphen von f und der x-Achse.
|
Klapptest mit ganzrationalen StammfunktionenHier kannst Du mit weiteren ganzrationalen Funktionsgleichungen |
Berechnung bestimmter Integrale mit StammfunktionenAn dieser Stelle solltest Du an einer umfangreicheren Aufgabenstellungen arbeiten. |
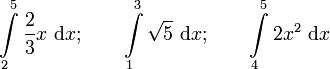
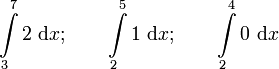
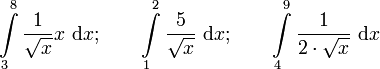
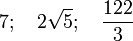
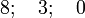
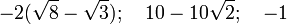
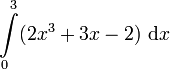
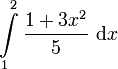
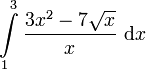

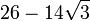
 .
Nach der Regel zur Intervalladditivität könnte auch ein einzelnes
Integral von der niedrigsten bis zur höchsten Nullstelle betrachtet
werden, wenn nach dem Wert des Integrals gefragt wäre. Jedoch ist nach
der Fläche gefragt. Deshalb müssen die Beträge der Integrale einzeln
betrachtet werden!!! Vergleiche dazu den Wert des Integrals in denselben
Grenzen, er ist 0.
.
Nach der Regel zur Intervalladditivität könnte auch ein einzelnes
Integral von der niedrigsten bis zur höchsten Nullstelle betrachtet
werden, wenn nach dem Wert des Integrals gefragt wäre. Jedoch ist nach
der Fläche gefragt. Deshalb müssen die Beträge der Integrale einzeln
betrachtet werden!!! Vergleiche dazu den Wert des Integrals in denselben
Grenzen, er ist 0.
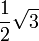 und
und 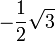 . Der Flächeninhalt hat den Wert
. Der Flächeninhalt hat den Wert 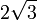 .
.
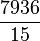 .
.