Das bestimmte Integral
Auf den vorigen Seiten hast Du gelernt, dass die Fläche A unter dem Graphen einer Funktion f(x) im Intervall [a;b] immer durch die Obersumme On und die Untersumme Un (jeweils bestehend aus n Rechtecksflächen) auf folgende Weise abgeschätzt werden kann:
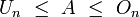
Diese Einschachtelung wird umso genauer, je mehr Rechteckflächen für
Ober- und Untersumme zur Anwendung kommen.
Die Trapezsumme ist der Mittelwert aus beiden Einschachtelungen.
Im Extremfall für 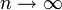 wird sie exakt. Es ergibt sich durch Grenzwertbetrachtung:
wird sie exakt. Es ergibt sich durch Grenzwertbetrachtung:
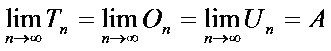
Nun ist es Zeit für eine wichtige Definition:
|
Definition
|
|
Merke:
Das Integralzeichen "∫"stellt ein stilisiertes S dar und steht für die unendliche Summe. Das "dx" ist ein sog. Differential
und bezeichnet die unendlich kleine Breite eines Rechtecks der Ober-
oder Untersumme beim Grenzübergang. Zusammenfassend bedeutet die
Integralschreibweise also den Grenzwert einer Summe. |
|
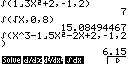
Berechne wieder mittels des Casio GTR das bestimmte Integral folgender
Funktionen in den jeweiligen Grenzen mittels ∫ (f(x) ,a,b) im RUN-Modus (RUN/OPT/CALC/ ∫ dx ) eingibst.
|
|
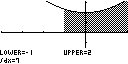
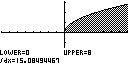
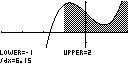
Berechne wieder mit Geogebra das bestimmte Integral folgender
Funktionen in den jeweiligen Grenzen, indem Du zuerst die Funktion f(x), die Intervallgrenzen a und b und dann den Befehl "A = Integral[f,a,b]" eingibst. Das Ergebnis wird Dir als Zahl "A" in der markierten Fläche und links im Algebra-Fenster angezeigt.
|
|
Im Applet unten sollst Du folgende Aufgaben bearbeiten:
|
|
Information für den LK: Berechnung des bestimmten Integrals mittels Grenzwertüberlegungen
An dieser Stelle sollst Du einmal das bestimmte Integral anhand eines
einfachen Beispiels selbst mittels Grenzwertüberlegungen von Hand berechnen. Dies ist nicht einfach
und kann in jedem Fall auch in Zusammenarbeit innerhalb einer Gruppe
geschehen!
Die Berechnung soll Dir aber einen vertiefenden Einblick in die
Berechnung des bestimmten Integrals geben und Dir verdeutlichen, dass
einfache Regeln zur Integration (Berechnung eines Integrals) eine wirkliche Vereinfachung darstellen.
Das erste Arbeitsblatt ist zur Bearbeitung durch Ausfüllen der Lücken
gedacht, während das zweite Arbeitsblatt dem reinen Durcharbeiten dient.
|
Navigation |
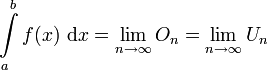

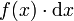 ist dann der Flächeninhalt (Höhe
ist dann der Flächeninhalt (Höhe  Breite) der unendlich schmalen Rechtecke!
Breite) der unendlich schmalen Rechtecke!
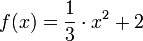 im Intervall
im Intervall 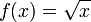 im Intervall
im Intervall 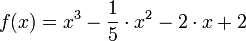 im Intervall
im Intervall